| Factorizing Q

$Q$ 라고 하는 것이 어떠한 포맷이 되었으면 좋겠는가 이에 대한 명확한 정의를 해본 적은 없었다.
$Q$ 는 어떠한 포맷이 되어도 상관이 없고, 가급적 단순한 형태였으면 좋겠다.
궁극적으로 하려고 하는 것은
$$Q(H \mid E, \lambda) = P(H \mid E, \theta)$$
그럼 $Q$ 의 가장 좋은 후보는 $P$ 와 동일한 확률분포함수, $\lambda$ 도 $\theta$ 와 동일하게 ...
하지만 $P$ 가 복잡하니깐 단순화시키겠다 ...
$Q$는 어떠한 approximation 형태
일단 마음대로 잡아놓고
Approximation 의 차이를 $\lambda$ optimization 을 통해 최대한 줄여보는 방식으로 인퍼런스 진행!
Mean Field Approximation
마음대로 잡을 수 있으니 아래와 같이 잡아보자
$$Q(H) = \prod_{i \leq \mid H \mid } q_{i}(H_{i} \mid \lambda_{i})$$
$q_{i}$ : Hidden 들의 각 개별적 확률 분포
개별적 variational parameter ($\lambda_{i}$) 가 주어진 상황에서는 $q_{i}$ 가 모두 각각 독립적이라고 가정 (단순 곱셈)
엄청나게 간단한 확률 분포를 만들어주는 강력한 가정
마치 Hidden variables 사이의 연관성을 없애버리는 것 - Approximation 할 때는 모든 연관관계를 다 빼버리겠다라는 것
대신 서로 묶인 게 없어지니깐 다루기가 훨씬 쉬워짐
$$P(H_{3}) \cdot P(H_{1} \mid H_{3}) \cdot P(H_{2}) $$
~
$$ q_{3}(H_{3} \mid \lambda) \cdot q_{1}(H_{1} \mid \lambda) \cdot q_{2} (H_{2} \mid \lambda) $$
$\lambda$ 가 주어지면 conditional 조건이 모두 필요하지 않다라는 가정
| Focusing on Single Variable in Q
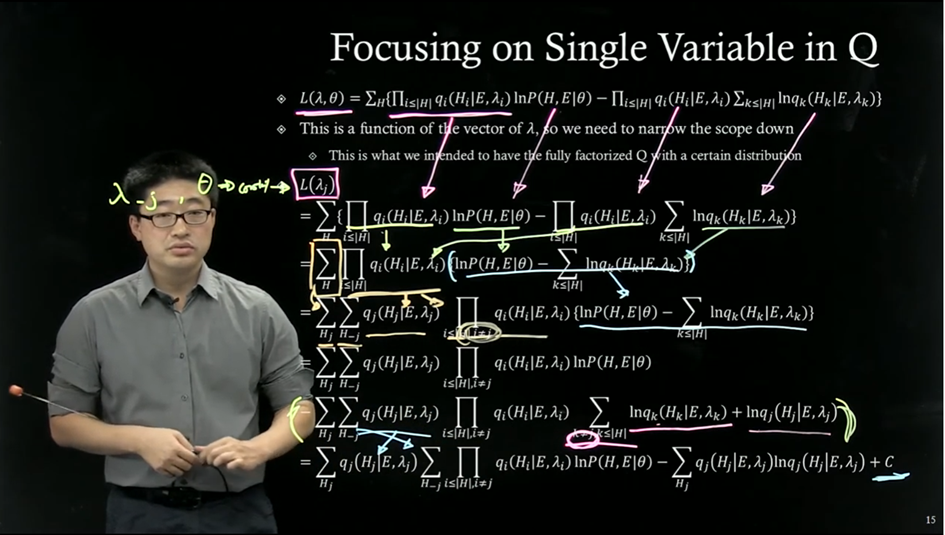
Mean filed approximation 통해서 → 개별 Hidden variable 들의 distribution 으로 쪼개진 형태 모델링
Whole set $\lambda$ 를 개별적 $\lambda$ 로 optimization 하는 형태로 바뀜
$\lambda_j$ 관점의 ELBO 다시 써보면 ...
$\lambda_{-j}$ 그리고 $\theta$ 는 constant 로 보고 ...
$\textup{ln} P(H, E \mid \theta) $ 는 쪼개지 않고 내비두고 ...
(위의 전개)
| Freeform Optimization

위에서 뒤쪽 텀은 어느정도 정리했고 여기서는 앞에 텀을 정리해보려는데 ...
새로운 $\tilde{P}$ function 을 정의한다고 생각해보자!
그렇게 하면 Weighted Average - Expectation 형태로 나타낼 수 있음
즉 완전한 $q$ 에 대해서 다 정의한 건 아니고
$j$ 번째에 대해서는 정의되지 않은 $q$ 를 이용하여 $P$ 에 대한 Expectation 계산한 것
그렇게 하면 $q_{i} (H_{i} \mid E, \lambda_{i} ) $ 와 $\tilde{P} (H, E \mid \theta)$ 의 KL Divergence 형태!
$\lambda$ 를 조정해서 만들 수 있는 $q_{i}^{\ *}$ 라는 것은 $\tilde{P}$ 와 동일하고
특정 Hidden variable 의 variational parameter optimization 한다는 것은!
그 특정한 hidden variable 을 뺀 나머지 variable 홀드하고 $P$ 라는 확률모델이 주어진 상황에서의 Expectation 에 대해 optimization 하는 것과 동일하다!
즉 나중에 $ln q_{i}^{\ *}$ 미분 0 계산하는 것을 Expectation 미분 0 계산하는 걸로 풀면 되겠다.
첫 번째 $i$ 에서부터 $\lambda$ 개수만큼 개별적으로 다 최적화해서
$q_{1}^{\ *}$, ... , $q_{n}^{\ *}$ 까지 다 만들어 주는 것 ...
제안한 확률모델의 Hidden 과 Evidence 를 활용해서 Expectation 을 찾고,
그 Expectation 을 최대화시켜줄 수 있도록 $\lambda$ 를 잡아보겠다!
Reference
문일철 교수님 강의
https://www.youtube.com/watch?v=T6hq5yIonqs&list=PLbhbGI_ppZIRPeAjprW9u9A46IJlGFdLn&index=5
'Study > Lecture - Advance 1' 카테고리의 다른 글
| W2.L6-9. Simple Example Model (0) | 2023.10.26 |
|---|---|
| W1.L1-5. 중간 Summary (0) | 2023.06.30 |
| W1.L4. VI - ELBO (0) | 2023.06.30 |
| W1.L3. VI - ln P(E) formulation (0) | 2023.06.30 |
| W1.L2. VI - Convex Duality, Applying Probability Function (0) | 2023.06.30 |



