L12 | Exponential Family
ELBO 더 하기 전에 Dirichlet 분포의 특성에 대해 조금 더 알아보자.
Dirichlet ... Beta distribution 의 연장선

$ \theta_{i} \sim \textup{Dir}(\alpha) $: $ \theta_{i} $ 라는 것이 이 분포에서 하나 sampling 되어 하나의 경우가 발생
이러한 경우라는 것이 얼마나 자주? 혹은 적게? 발생할 것이냐에 대한 설명이 필요 ... PDF ... $ \textup{P}(\theta_{i} \mid \alpha) $
Dirichlet Dist. 라는 것은 위 조건들을 만족하는 상황에서 정의
Probability Simplex를 잘 만족 ... 이 말은 여기 분포에서 나온 $X$ 는 확률로 잘 사용될 수 있다.
... $X$ 는 multinomial dist. 에서 parameter 로 잘 쓰일 수 있다.
... (압정 위 0.6 / 아래 0.4) ... 0.6 과 0.4 라는 parameters → Dir. 에서 설명할 수 있다.
예를 들어 $(\alpha_{1}, \alpha_{2}, \alpha_{3}) = (1, 1, 1) $ 의 경우 ... 모두 1/3 확률 ... $\alpha$ 에 따라 그 모양이 결정

위 수식의 형태와 같이 표현되면 "Exponential Family"
$T(x)$ : Sufficient statistics. 실제 많은 정보 ($x$) 들이 활용되는 부분
$h(x)$ : Underlying measure. 확률로 만들어주기 위한 normalization 성분
$\eta(\theta)$ : Natural parameter. 평균과 같이 특정한 의미 있는 파라미터를 formation 하는 효과
$A(\theta)$ : Log normalizer. 이 또한 normalization 성분
Derrivative of log normalizer - Moment of sufficient statitics
Log normalizer 미분은 Sufficient statistics의 기대값!
L13 | Derivation of the first term
다시 ELBO 로 돌아와서 첫 번째 Expectation term 유도

$\gamma, \phi, \alpha, \beta$ 총 4 가지 ... 우리가 학습을 통해 "최적화" 해야될 parameters

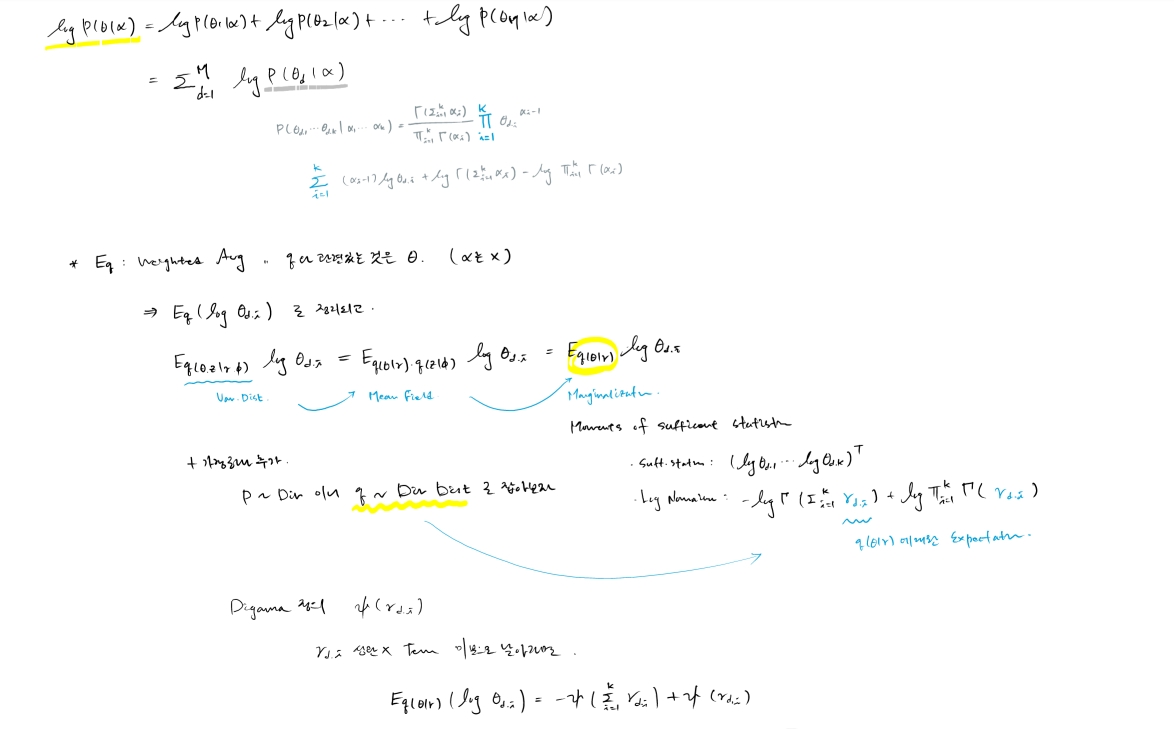
이로서 가장 첫 번째 term derivation 완료
Reference
문일철 교수님 강의
https://www.youtube.com/watch?v=qBoPMaWxAKc&list=PLzZ7PPT4KK5qpd-1VF4qmFMlpnr1is7Pu&index=50
'Study > Lecture - Advance 1' 카테고리의 다른 글
| W3.L16-17. Optimization of ELBO (0) | 2023.11.29 |
|---|---|
| W3.L14-15. Derivation of the other terms (0) | 2023.11.28 |
| W3.L10-11. Latent Dirichlet Allocation (LDA) (0) | 2023.11.07 |
| W2.L6-9. 중간 Summary (0) | 2023.11.05 |
| W2.L6-9. Simple Example Model (0) | 2023.10.26 |



