W8.L8-9. Gaussian Mixture Model - EM Algorithm
| Inference with Latent Variables
Difference between classification and clustering
Complete set of variables: { $X, Z$ }
$X$ : observed variables
$Z$ : hidden (latent) variables
$\theta$ : parameters for distributions
Classification (supervised learning)
$ P(X \mid \theta) $ → $ \textup{ln}\ P(X \mid \theta) $
Clustering (unsupervised learning)
모르는 녀석 $Z$ 를 어떻게 하면 좋을까 라는 고민이 함께 필요
$ P(X \mid \theta) = \sum_{Z} P(X, Z \mid \theta) $ → $ \textup{ln}\ P(X \mid \theta) = \textup{ln}\ \left\{ \sum_{Z} P (X, Z \mid \theta) \right\} $
Log 안에 Summation 계산 ... 최적화하기 어려운 형태 !
이걸 어떻게 풀거냐 했을 때 ...
우리가 모르는 두 가지 변수 $Z$ 와 $\theta$ 를 iteratively 계산하면서
$P(X \mid \theta) = \sum_{Z} P(X, Z \mid \theta)$ 확률을 최적화 하는 방법! : EM Algorithm
| Probability Decomposition
ML : 눈에 보이는 Data X 에서 $\theta$ 를 최적화해서 알아내는 것
그냥 $P(X \mid \theta) $ 를 계산하는게 어려워서 $\textup{ln}\ P(X \mid \theta) $ 를 계산!

| Maximizing the Lower Bound

요약하면 ...
$$l(\theta)=lnP(X \mid \theta)=ln\left\{ \sum_{Z}q(Z)\cdot \frac{P(X,Z \mid \theta)}{q(Z)} \right\} \geq \sum_{Z}q(Z)\cdot ln\frac{P(X,Z \mid \theta)}{q(Z)}$$
여기서 Lower Bound 를 두 가지 형태 $Q(\theta, q)$ 와 $L(\theta, q)$ 로 정의 가능
$$
\begin{align*}
Q(\theta, q) &=E_{q(Z)}ln P(X, Z \mid \theta) + H(q) \\
\\
L(\theta, q) &= ln P(X \mid \theta)-\sum_{Z} \left\{ q(Z) \cdot ln \frac{q(Z)}{P(Z\mid X, \theta)}\right\} \\
&= ln P(X\mid \theta) - KL(q(Z) \parallel P(Z \mid X, \theta)) \\
\end{align*}
$$
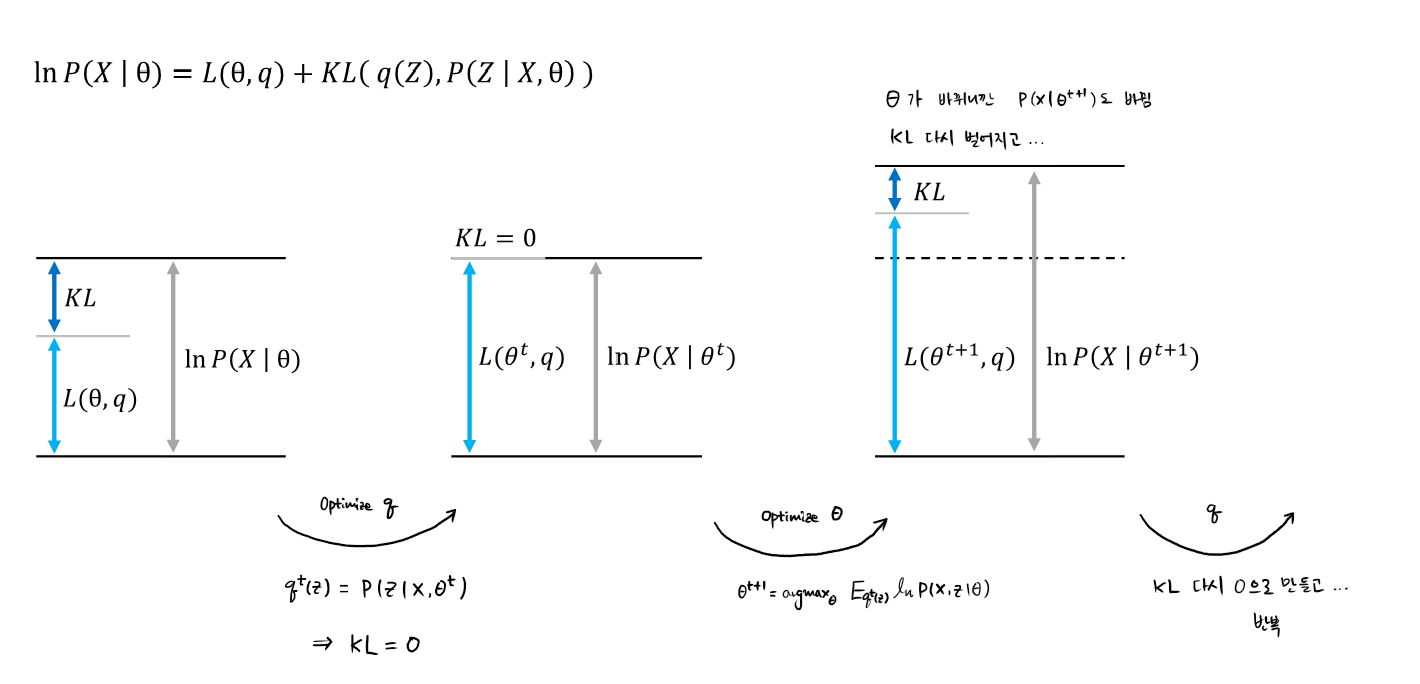
$L(\theta, q)$ 를 살펴보면 ...
The first term is fixed when $\theta$ is fixed at time $t$
The second term can be minimized to maximize $L(\theta, q)$
$$q^{t}(Z)=P(Z \mid X,\ \theta^{t}) \ \ \rightarrow \ \ KL\left ( q(Z) \parallel P(Z \mid X,\ \theta) \right )=0$$
즉, 특정 시간 $t$, 특정 iteration 에서의
$q^{t}(Z)$ 를 $P(Z\mid X, \ \theta^{t})$ 로 받아들이면,
Lower bound 가 최대화되면서 Equality 로 되겠다!
(Assignment probability 로 받아들이겠다.)
이러한 사실을 $Q(\theta, q)$ 에 대입해보면 ...
$$Q(\theta, q^{t}) = E_{q^{t}(Z)}ln P(X, Z \mid \theta^{t}) + H(q^{t})$$
Optimizing $\theta$ ...
$$ \theta^{t+1}=argmax_{\theta}\ Q(\theta, q^{t}) = argmax_{\theta}\ E_{q^{t}(Z)}ln P(X, Z \mid \theta^{t}) $$
| EM Algorithm
특정 $t$ 에서 $\theta$ 가 정해져있을 경우, $q^{t}(Z)$ Z 에 대한 Distribution 을 알아낼 수 있었고,
이를 통해 $Q(\theta, q)$ 를 최적화하여 $\theta^{t+1}$ 을 새로 찾아낼 수 있다.
아래 두 가지를 반복하는 것이 EM !!!
$q^{t}(Z)=P(Z \mid X,\ \theta^{t})$ ... KL Divergence 를 활용해서 Latent variable Z 의 Probability Distribution 을 알아내는 것
$q^{t}(Z)$ 를 대입하여 $\theta$ 를 다시 Update 하는 것
Initial value 에 따라 local minima 빠지기도 ...
Practical 성능이 좋아서 많은 모델에서 활용 ...

| SUMMARY
Finds the maximum likelihood solutions for models with latent variables
이걸 Optimization 하려니 ... 쉽지 않았다 ...
$$
\begin{align*}
P(X \mid \theta)&=\sum_{Z}P(X, Z \mid \theta) \\
ln P(X \mid \theta)&=ln \left\{ \sum_{Z}P(X, Z \mid \theta)\right\}
\end{align*}
$$
EM Algorithm
Initialize $\theta^{0}$ to an arbitrary point
Loop until the likelihood converges
- Expectation step
* $q^{t+1}(Z)=argmin_{q}\ KL(\ q(Z)\parallel P(Z \mid X,\ \theta)\ )$
→ $q^{t}(Z)=P(Z \mid X,\ \theta)$
... Assign $Z$ by $P(Z \mid X,\ \theta)$
- Maximization step
* $\theta^{t+1}=argmax_{\theta}\ Q(\theta, q^{t}) = argmax_{\theta}\ E_{q^{t}(Z)}ln P(X, Z \mid \theta^{t}) $
* Fixed $Z$ means that there is no unobserved variables
* Same optimization of ordinary MLE
Reference
문일철 교수님 강의
https://www.youtube.com/watch?v=mnUcZbT5E28&list=PLbhbGI_ppZISMV4tAWHlytBqNq1-lb8bz&index=55
https://www.youtube.com/watch?v=mnUcZbT5E28&list=PLbhbGI_ppZISMV4tAWHlytBqNq1-lb8bz&index=56